가장 쉽게 설명하는 - 볼록 껍질 (Convex Hull)

Posted Feb 2, 2025 Updated Feb 19, 2025

By GreenScreen410

15 min read

개요

사진 출처: https://david0506.tistory.com/62

볼록 껍질(Convex Hull)은 점들이 주어졌을 때 모든 점을 포함하는 볼록 다각형을 구성하는 알고리즘으로, 주로 특정 상황에서의 최소 다각형을 구하는데 사용되곤 합니다.
여기서 볼록 다각형이란, 모든 내각이 180도 이하로만 이루어진 다각형을 말합니다.

볼록 껍질을 구하는데에는 다양한 알고리즘이 사용되지만, 대표적으로 그레이엄 스캔과 앤드류 모노톤 체인이 사용됩니다.
그레이엄 스캔은 보다 유연한 각도 조정이 가능하다는 장점과, 앤드류 모노톤 체인은 코드가 간결하다는 장점이 있습니다.

그레이엄 스캔 (Graham Scan)

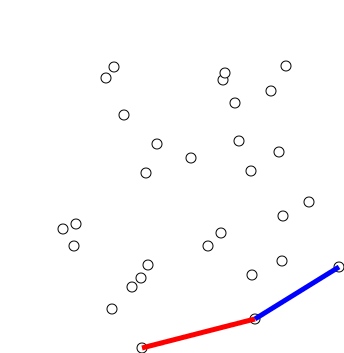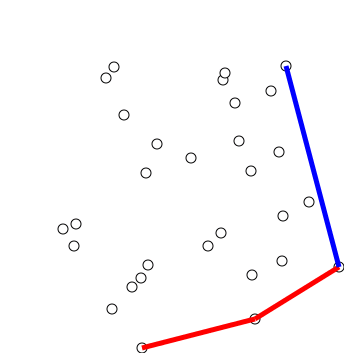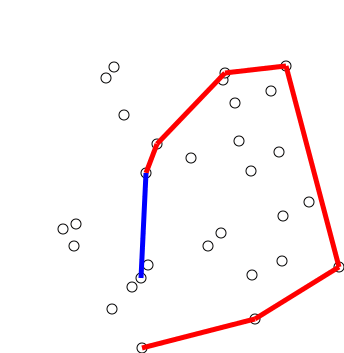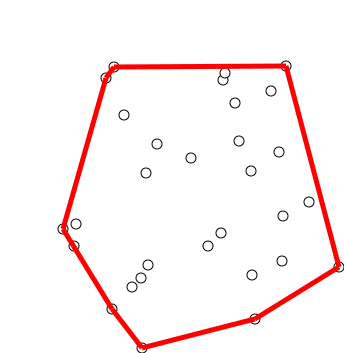사진 출처: https://en.wikipedia.org/wiki/File:GrahamScanDemo.gif

그레이엄 스캔은 $O(N \log N)$의 시간 복잡도를 가지는 알고리즘으로, 스택을 사용하여 구현합니다.

C++의 vector와 같이 스택과 동일한 역할을 수행할 수 있는 자료 구조를 사용해도 됩니다.

반시계 방향으로 정렬하기

  
sort(points.begin(), points.end(), [](Point a, Point b) {
  return make_pair(a.y, a.x) < make_pair(b.y, b.x);
});

점들을 정렬하는 과정이 왜 필요하냐고 할 수 있는데, 그래야 모든 점들을 바깥부터, 반시계 방향으로 탐색할 수 있기 때문입니다. (물론 시계방향으로 탐색할 수도 있습니다.)
일종의 탐색하는 순서를 매겨주는 과정이러고 볼 수 있습니다.

먼저, y좌표가 작은 순서대로, y좌표가 같으면 x좌표가 작은 순서대로 점들을 정렬합니다.
람다 함수와 make_pair를 통해 별도의 compare 함수를 생성하지 않고, 매우 직관적이게 한 줄로 정렬을 끝낼 수 있습니다.

  
Point pivot = points.front();
sort(points.begin() + 1, points.end(), [pivot](Point a, Point b) {
  if (ccw(pivot, a, b) > 0) return true;
  else if (ccw(pivot, a, b) < 0) return false;
  else return make_pair(a.y, a.x) < make_pair(b.y, b.x);
});

y좌표를 기준으로 정렬하면 자연스럽게 points의 첫 번째 원소(points.front())인 pivot은 y좌표가 가장 낮은 점이 되는데, 이 pivot을 기준으로 CCW 값이 양수인 방향으로 점을 정렬합니다.
(CCW 값이 양수라는 뜻은, 쉽게 말해 선분이 바깥으로 굽는다는 뜻입니다.)

만약 양수도, 음수도 아니라면(일직선상에 있다면) 좌표 순서대로 정렬합니다.

볼록 껍질 완성하기

  
vector<Point> hull;
for (auto p : points) {
  while (hull.size() >= 2 && ccw(hull[hull.size() - 2], hull.back(), p) <= 0) hull.pop_back();
  hull.push_back(p);
}

볼록 껍질을 이루는 점들의 좌표를 반환할 hull 벡터를 생성한 뒤, 이어서 아래 과정을 수행합니다.

처음에는 hull 벡터가 비어있기 때문에 while문이 실행되지 않고, hull.push_back(p)가 그대로 실행됩니다.
점이 두 개 모인 후부터 while문이 실행됩니다. hull의 마지막 두 점(hull[hull.size() - 2], hull.back())과 현재 점 p를 확인합니다.
점 p를 hull에 추가하기 전, 만약 이 세 점이 시계 방향, 또는 일직선상에 배치되어 있으면(즉, CCW 값이 0 이하일 경우), 마지막 점은 볼록 껍질에 포함될 수 없으므로 pop_back()으로 제거합니다. 이 과정을 통해 적합하지 않은 점 p를 모두 제거합니다.
일부 문제에서는 일직선상에 있는 모든 점을 볼록 껍질에 포함시켜야 할 수도 있습니다.
~~해당 문제는 엄밀히 말하자면 볼록 껍질 문제는 아닙니다.~~
이 과정을 전체 점들에 대해 반복하면, 최종적으로 hull에는 볼록 껍질을 이루는 점들만 순서대로 남게 됩니다.

코드

  
struct Point {
  long long x, y;
};

long long ccw(Point a, Point b, Point c) {
  return (a.x * b.y + b.x * c.y + c.x * a.y) - (a.y * b.x + b.y * c.x + c.y * a.x);
}

vector<Point> convex_hull(vector<Point> points) {
  sort(points.begin(), points.end(), [](Point a, Point b) {
    return make_pair(a.y, a.x) < make_pair(b.y, b.x);
  });

  Point pivot = points.front();
  sort(points.begin() + 1, points.end(), [pivot](Point a, Point b) {
    if (ccw(pivot, a, b) > 0) return true;
    else if (ccw(pivot, a, b) < 0) return false;
    else return make_pair(a.y, a.x) < make_pair(b.y, b.x);
  });

  vector<Point> hull;
  for (auto p : points) {
    while (hull.size() >= 2 && ccw(hull[hull.size() - 2], hull.back(), p) <= 0) hull.pop_back();
    hull.push_back(p);
  }

  return hull;
}

코드 (간소화)

연산자 재정의를 통하여 정렬 과정을 단순화 하였습니다.

  
struct Point {
  long long x, y;
  
  bool operator<(Point other) { return x == other.x ? y < other.y : x < other.x; }
};

long long ccw(Point a, Point b, Point c) {
  return (a.x * b.y + b.x * c.y + c.x * a.y) - (a.y * b.x + b.y * c.x + c.y * a.x);
}

vector<Point> convex_hull(vector<Point> points) {
  sort(points.begin(), points.end());
  sort(points.begin() + 1, points.end(), [p = points.front()](Point a, Point b) {
    return ccw(a, b, p) ? ccw(a, b, p) > 0 : a < b;
  });

  vector<Point> hull;
  for (auto p : points) {
    while (hull.size() >= 2 && ccw(end(hull)[-2], hull.back(), p) <= 0) hull.pop_back();
    hull.push_back(p);
  }

  return hull;
}

앤드류 모노톤 체인 (Andrew’s Monotone Chain)

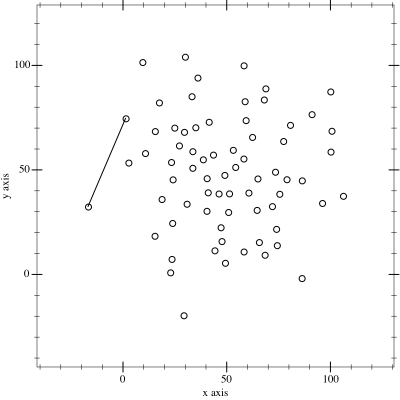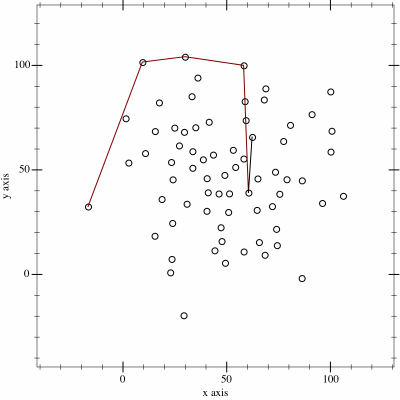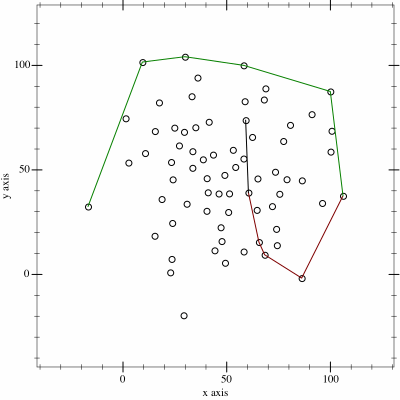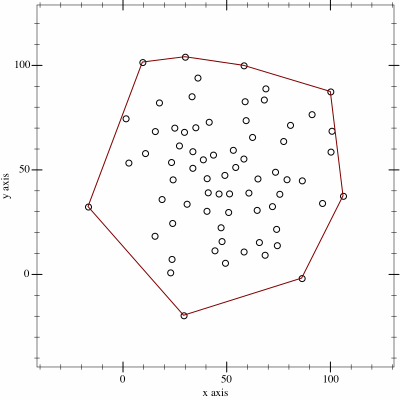사진 출처: https://upload.wikimedia.org/wikipedia/commons/9/9a/Animation_depicting_the_Monotone_algorithm.gif

앤드류 모노톤 체인은 $O(N \log N)$의 시간 복잡도를 가지는 알고리즘이며, 그레이엄 스캔의 작동 방식과 매우 유사합니다.

x좌표에 대해 정렬하기

  
sort(points.begin(), points.end(), [](Point a, Point b) {
  return make_pair(a.x, a.y) < make_pair(b.x, b.y);
});

앤드류 모노톤 체인은 모든 점을 왼쪽부터 오른쪽으로 탐색한다는 아이디어를 가지고 있습니다.
그레이엄 스캔과 정 반대로, x좌표가 작은 순서대로, x좌표가 같으면 y좌표가 작은 순서대로 점들을 정렬합니다.

위쪽 껍질, 아래쪽 껍질

  
vector<Point> hull;
for (auto p : points) {
  while (hull.size() >= 2 && ccw(hull[hull.size() - 2], hull.back(), p) <= 0) hull.pop_back();
  hull.push_back(p);
}

int lower_hull_size = hull.size();
for (int i = points.size() - 2; i >= 0; i--) {
  while (hull.size() > lower_hull_size && ccw(hull[hull.size() - 2], hull.back(), points[i]) <= 0) hull.pop_back();
  hull.push_back(points[i]);
}
hull.pop_back();

모든 점들을 정렬한 후, 두 개의 볼록 껍질(위쪽과 아래쪽)을 각각 만들어 나갑니다. 이렇게 만들어진 위쪽 껍질과 아래쪽 껍질을 합치면 전체 볼록 껍질을 구성하게 됩니다.

정렬된 점들을 순회하며 첫 번째 루프에서는 아래쪽 껍질을 만듭니다. 그레이엄 스캔과 100% 동일한 과정입니다.
이어서 두 번째 루프에서는 오른쪽에서 왼쪽으로 점들을 순회하며 위쪽 껍질을 만듭니다. 이때, 아래쪽 껍질과 충돌하지 않도록 lower_hull_size 변수를 만들어 조건을 설정합니다.
마지막으로, 서로 시작점이 중복되므로 이를 제거하면 전체 볼록 껍질이 완성됩니다.

코드

  
struct Point {
  long long x, y;
};

long long ccw(Point a, Point b, Point c) {
  return (a.x * b.y + b.x * c.y + c.x * a.y) - (a.y * b.x + b.y * c.x + c.y * a.x);
}

vector<Point> convex_hull(vector<Point> points) {
  sort(points.begin(), points.end(), [](Point a, Point b) {
    return make_pair(a.x, a.y) < make_pair(b.x, b.y);
  });
  
  vector<Point> lower, upper;
  for (auto p : points) {
    while (lower.size() >= 2 && ccw(lower[lower.size() - 2], lower.back(), p) <= 0) lower.pop_back();
    lower.push_back(p);
  }
  
  for (int i = points.size() - 1; i >= 0; i--) {
    while (upper.size() >= 2 && ccw(upper[upper.size() - 2], upper.back(), points[i]) <= 0) upper.pop_back();
    upper.push_back(points[i]);
  }
  
  lower.pop_back();
  upper.pop_back();
  lower.insert(lower.end(), upper.begin(), upper.end());
  
  return lower;
}

해결할 수 있는 문제

위 볼록 껍질 코드만 잘 이해해도 풀 수 있는 문제가 엄청나게 많습니다!
코드는 그레이엄 스캔을 기준으로 작성되었습니다.

1708 - 볼록 껍질

가장 기초적인 문제로, 볼록 껍질을 구성하는 점의 개수를 출력하는 문제입니다.

2254 - 감옥 건설

해당 문제는 ‘볼록 다각형 내 점 판정’ 알고리즘을 알고 있어야 합니다.

점 $(P_x, P_y)$가 몇 번째 볼록 껍질에 있는지 구하는 문제로, vector<vector<Point>> 벡터를 만들어 해결할 수 있습니다.

해당 문제는 ‘볼록 다각형 내 점 판정’ 알고리즘을 알고 있어야 합니다.

2254와 비슷하게, 몇 번째 볼록 껍질에 속해 있는지에 따라서 점수를 더해 주면 됩니다.

26179 - Faster Than Light

단순 볼록 껍질 문제 치고는 높은 난이도를 가지고 있는 문제입니다. (다이아몬드 3)
(추후 해설 작성 예정)

Algorithm, Geometry

This post is licensed under CC BY 4.0 by the author.

가장 쉽게 설명하는 - 볼록 껍질 (Convex Hull)

개요

그레이엄 스캔 (Graham Scan)

반시계 방향으로 정렬하기

볼록 껍질 완성하기

코드

코드 (간소화)

앤드류 모노톤 체인 (Andrew’s Monotone Chain)

x좌표에 대해 정렬하기

위쪽 껍질, 아래쪽 껍질

코드

해결할 수 있는 문제

1708 - 볼록 껍질

2254 - 감옥 건설

2699 - 격자점 컨벡스헐

6194 - Building the Moat

6850 - Cows

6962 - Maple Roundup

7420 - 맹독 방벽

9737 - Area Between Outer Hull and Inner Hull

10903 - Wall construction

21624 - Fence

27656 - 양궁

26179 - Faster Than Light